4 Irrigação por Aspersão

A aspersão é o método de irrigação em que a água é aspergida sobre a superfície do terreno e assemelha-se a uma chuva.

A passagem da água sob pressão pelos bocais dos asperores causa o fracionamento do jato de água que atinge o solo, onde se infiltra e permanece disponível para utilização pelas plantas.

4.1 Adaptabilidade da Irrigação por Aspersão

Os sistemas de irrigação por aspersão podem ser dos mais variados tipos, possuindo uma ampla gama de características e capacidades que os torna adequados para praticamente todas as culturas e todos os tipos de solo.

O maior cuidado que se deve ter é quando as irrigações são de alta intensidade, que podem levar a escoamento superficial indesejado. A escolha do aspersor deve ser muito criteriosa para não causar este tipo de problema.

Também poderão haver problemas se a irrigação for realizada em condições de alta temperatura e baixa umidade do ar, que podem levar a grandes perdas pela evaporação da água, ou quando for realizada em condições de alto velocidade do vento, que causa perda por deriva.

Além disso, o molhamento foliar pode causar problemas fitossanitários, como a proliferação de doenças. Os jatos de água que saem do aspersor podem causar danos aos frutos e queda das flores.

E por último, deve ser levado em consideração os custos da irrigação, tanto o investimento inicial no dimensionamento, aquisição e instalação dos equipamentos, quanto os gastos com energia para pressurização do sistema.

4.2 Componentes de um sistema de irrigação por aspersão

Os sistemas de irrigação por aspersão necessitam via de regra, de:

Um conjunto motobomba para pressurização
Tubulações para transporte da água
Aspersores para distribuição da água

4.2.1 Tubulações

Para o transporte da água do conjunto motobomba até o sistema de irrigação, podem existir várias tubulações que recebem nomes especiais conforma sua localização. A linha adutora é aquela que liga o conjunto motobomba até o início da área irrigada. A linha principal é uma continuidade da linha adutora, dentro da área irrigada. Desta, partem as linhas de derivação. Por fim, existem as linhas laterais, as mais importantes do sistema, pois nelas estão instalados os aspersores. Estas deve ser instaladas paralelas às curvas de nível e perpendiculares aos ventos predominantes.

Com exceção das linhas laterais, as outras linhas podem ou não existir em um sistema de aspersão.

Os materiais mais utilizados nas tubulações em sistemas de aspersão são:

Metálicos: aço zincado, alumínio, ferro fundido;
Plásticos: PVC (cloreto de polivinila) e PE (polietileno).

4.2.2 Aspersores

São a parte mais importante do sistema, responsáveis pela distribuição uniforme da água na área irrigada.

Podem ser grandes aspersores metálicos, taméem conhecidos como canhão, até pequenos aspersores de plástico ou metal.

Timhall. / CC BY-SA

Anton / CC BY-SA

JJ Harrison (https://www.jjharrison.com.au/) If you enjoy my work, and would like to see more, please subscribe to my profile on Facebook. / CC BY-SA

Podem ser classificadoas quanto à rotação em:

Aspersores rotativos de giro completo: quando irrigam um círculo completo
Aspersores setoriais: quando não irrigam um círculo completo, que pode ser uma meia-lua (180°) ou um canto (90°). São utilizado em setores periféricos do sistema.

Quanto ao ângulo de inclinação:

30°
6° (subcopa)

Quanto ao número de bocais:

Simples
Duplo

Quanto à pressão de serviço:

Muito baixa – 4 a 10 mca
Baixa – 10 a 20 mca
Média – 20 a 40 mca
Gigante - 40 a 80 mca

4.3 Disposição dos aspersores

Um aspersor tem um perfil de distribuição desuniforme no círculo molhado, com uma intensidade de aplicação maior próxima ao centro e menor aplicação nas bordas.

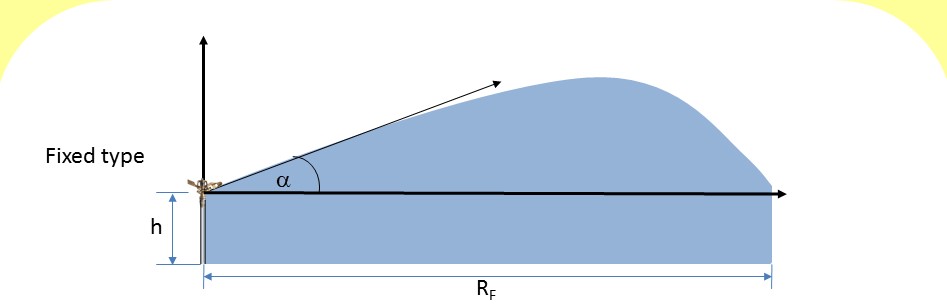
Para garantir uniformidade deve haver sobreposição da áreas molhada entre aspersores adjacentes. Uma recomendação é que seja de cerca de 65% de sobreposição do raio molhado, mas este valor pode varia conforme o projeto.

4.4 Escolha do aspersor

O principal fator de escolha do aspersor é a intensidade de aplicação, que deve ser menor que a velocidade de infiltração básica do solo (VIB):

\[ Ia_{aspersor} \leq VIB_{solo} \]

A intensidade de aplicação de um aspersor pode ser calculada pela equação:

\[ I_a = \frac{Q_a}{E_l \cdot E_a} \]

Em que:

Q_a - vazão do aspersor
E_l - Espaçamento entre linhas laterais
E_a - Espaçamento entre aspersores

Exemplo 4.1 (Escolha do aspersor.) Considere os aspersores listados abaixo. Defina qual poderia ser utilizado em uma área cujo solo possui uma VIB de 10 mm/h.

	Aspersor 1	Aspersor 2
Pressão (mca)	30	20
Vazão (m3/h)	10,6	2,1
Espaçamento(m)	30x30	18x18

\(Ia_1 = \frac{10,6}{30 \cdot 30} \cdot 1000 = 11,7 mm/h\)

\(Ia_2 = \frac{2,1}{18 \cdot 18} \cdot 1000 = 6,5 mm/h\)

O aspersor 1 não é adequado pois possui Ia maior que a VIB do solo. O aspersor 2, pelo contrário, pode ser utilizado.

4.5 Relação pressão x vazão x diâmetro do bocal do aspersor

A vazão de um bocal pode ser calculada pela equação:

\[ Q = C_d \cdot A \cdot \sqrt{2 \cdot g \cdot P_s} \]

Para um mesmo aspersor, mantendo o C_d e o diâmetro (área) do bocal constante, a relação entre vazão e pressão é:

\[ \frac{Q_1}{Q_2} = \frac{\sqrt{P_1}}{\sqrt{P_2}} \]

Exemplo 4.2 (Relação Pressão-Vazão.) Um aspersor fornece 1 m³/h a uma pressão de serviço de 20 mca. Qual deve ser a pressão para aumentar a vazão em 50%?

\(\frac{1}{1,5} = \frac{\sqrt{20}}{\sqrt{P_2}}\)

\(P_2 = 45 mca\)

Para um mesmo aspersor, mantendo o C_d e a pressão de serviço constante, a relação entre vazão e diâmetro do bocal é:

\[ \frac{Q_1}{Q_2} = \frac{D_1^2}{D_2^2} \]

Exemplo 4.3 (Relação Vazão-Diâmetro.) Considere o seguinte aspersor:

Vazão – 2 m³/h
Bocal – 6 mm de diâmetro
Pressão de serviço – 30 mca

Determine a nova vazão considerando-se a troca do bocal de 6 mm para outro bocal de 8 mm

\(\frac{2}{Q_2} = \frac{6^2}{8^2}\)

\(Q_2 = 3,6 m^3/h\)

4.6 Pivô Central

É um sistema de movimentação circular auto propelido, composto por uma única linha lateral com vários aspersores que gira apoiada em um ponto fixo. O comprimento da linha lateral pode ser de 200 a 800 m, sendo mais comum de 400 m (EUA).

Tequask / CC BY-SA

Jeffrey Beall / CC BY

Workman / CC BY-SA

A tomada de água é feita por poços ou adutoras enterradas.

As torres são dotadas de rodas com um dispositivo de propulsão. A movimentação da linha lateral do pivô central acontece devido ao alinhamento e desalinhamento das torres. Quando as torres ficam desalinhadas, acionam a propulsão e se movimentam. O movimento cessa no momento em que as torres deixam de estar desalinhadas. Veja no vídeo abaixo:

A maior vantagem do pivô central é a economia de mão-de-obra, por tratar-se de um sistema de movimentação mecânica.

Por outro lado, há perda de área devido ao padrão circular de irrigação.

O maior problema é a alta intensidade de aplicação na extremidade do pivô, que pode causar escoamento superficial indesejado.

4.6.1 Intensidade de aplicação em pivô central

A intensidade de aplicação é variável em função da distância do ponto fixo do pivô. Quanto mais próximo do centro, menor é a intensidade de aplicação, devido ao menor perímetro que deve ser percorrido.

O tempo de aplicação (em horas) em um ponto é calculado por:

\[ t_r = \frac{H \cdot d}{2 \cdot \pi \cdot r} \]

em que

H - tempo para uma volta do pivô, em horas
d - diâmetro de cobertura do aspersor naquele ponto, em metros
r - distância do ponto ao centro do pivô, em metros

A intensidade de aplicação (em mm/h) é calculada por:

\[ I_a = \frac{L}{t_r} \]

em que

L - lâmina aplicada, mm

Exemplo 4.4 (Intensidade de aplicação.) Determinar a intensidade de precipitação a 50, 100, 200 e 400 m em um pivô com as seguintes características:

Lâmina aplicada: 7 mm/volta
Tempo da volta: 24 horas
Raio aspersor: 14 m

\(t_{r50} = \frac{24 \cdot 12 \cdot 2}{2 \cdot \pi \cdot 50} = 2,1 horas\)

\(I_{a50} = \frac{7}{2,1} = 3,3 mm/h\)

\(t_{r100} = \frac{24 \cdot 12 \cdot 2}{2 \cdot \pi \cdot 100} = 1,1 horas\)

\(I_{a100} = \frac{7}{1,1} = 6,4 mm/h\)

\(t_{r200} = \frac{24 \cdot 12 \cdot 2}{2 \cdot \pi \cdot 200} = 0,53 horas\)

\(I_{a200} = \frac{7}{0,53} = 13,2 mm/h\)

\(t_{r400} = \frac{24 \cdot 12 \cdot 2}{2 \cdot \pi \cdot 400} = 0,27 horas\)

\(I_{a400} = \frac{7}{0,27} = 25,9 mm/h\)

A velocidade de deslocamento de um pivô central é determinada pela última torre. Esta, se movimenta a uma velocidade constante, que pode ser regulada por meio de um percentímetro. A regulagem do percentímetro determina a proporção do tempo parada e em movimento da última torre. Por exemplo, para um percentímetro regulado em 75%, a última torre irá se mover 75% do tempo e irá permanecer parada 25% do tempo (anda 3 minutos e para 1 minuto). A regulagem máxima do percentímetro é de 100%, e neste regulagem o sistema irá aplicar a lâmina mínima por volta. Qualquer regulagem menor que 100% irá aumentar a lâmina aplicada.

Exemplo 4.5 (Operação de um pivo central.) Considere um pivô central com as seguintes características:

Velocidade da última torre: 240 m/h
Raio da última torre: 560 m
Vão em balanço: 20 m
Vazão: 346 m³/h
Funcionamento: 20 h/dia

Pede-se:

Área do pivô
Tempo para dar uma volta (período)
Lâmina aplicada por volta
Lâmina aplicada por dia de funcionamento
Lâmina aplicada por volta na regulagem de 80% e 90%
Supondo a necessidade de aplicar uma lâmina de 5 mm, determinar a regulagem do percentímetro

\(Area = \pi \cdot (560+20)^2 = 1056831 m^2 = 105 ha\)
\(Perimetro = 2 \cdot \pi \cdot 560 = 3518,6 m\)

\(T_{volta} = \frac{perimetro} {velocidade} = \frac{3518,6}{240} = 14,7 horas\)
\(lamina_{volta} = \frac{volume}{area} = \frac{346 \cdot 1000 \cdot 14.7}{1056831} = 4,8 mm/volta\)
\(Lamina_{dia} = \frac{346 \cdot 1000 \cdot 20}{1056831} = 6,5 mm/dia\)
\(Lamina_{80\%} = 100 \cdot 4,8 / 80 = 6 mm\)

\(Lamina_{90\%} = 100 \cdot 4,8 / 90 = 5,3 mm\)
\(Reg_{5mm} = 4,8 \cdot 100 / 5 = 96\%\)

4.7 Carretel enrolador

O carretel enrolador é composto por um canhão hidráulico montado sobre uma carretinha. O deslocamento se dá em virtude da ação do carretel que enrola a própria mangueira. É muito utilizado para aplicação de vinhaça (subproduto da indústria) nos cultivos de cana-de-açúcar.

Nick Birse / CC BY-SA

Oast House Archive / Field Sprayer

O giro do aspersor normalmente é regulado para um ângulo de 330°, de modo a manter seca a faixa de movimentação da carretinha com o aspersor.

Para uma faixa irrigada, a carretinha deve ser instalada para iniciar a irrigação a uma distância L_i (em metros) do início da área e deve parar a irrigação a uma distãncia L_f (em metros) do final da faixa irrigada.

\[ L_i = \frac{2}{3} \cdot R_i \]

em que:

R_i - raio irrigado pelo aspersor, em metros

\[ L_f = \frac{2}{3} \frac{w-180}{180} \cdot R_i \]

em que:

w - ângulo de giro do aspersor, em graus

Nestas posições, inicial e final, a carretinha com o aspersor deve ficar estacionada, realizando irrigação por um tempo T_i = T_f (em minutos):

\[ T_i = T_f = \frac{2}{3} \frac{w}{360} \frac{R_i}{V_d} \]

em que:

V_d - velocidade de deslocamento do equipamento, m/min

Exemplo 4.6 (Operação do carretel.) Considere um carretel enrolador:

Alcance do canhão - 60 m
Espaçamento – 96 m (80% de sobreposição)
Comprimento da faixa irrigada – 600 m
Ângulo de funcionamento – 330°
Vazão – 155,4 m³/h
Lâmina líquida de irrigação – 22 mm
Eficiência – 80%

Pede-se:

Comprimento das faixas inicial, intermediária e final
Velocidade de deslocamento na faixa intermediária
Tempo parado na faixa inicial e na faixa final
Tempo total de irrigação

\(L_i = \frac{2}{3} \cdot 60 = 40 m\)

\(L_f = \frac{2}{3} \frac{330 - 180}{180} \cdot 60 = 33 m\)

\(L_{int} = 600 - 40 - 33 = 527 m\)

\(T_{int} = \frac{Area \cdot Lamina}{Q} = \frac{96 \cdot 527 \cdot 22/0,80}{155,4 \cdot 1000} = 8,95 horas\)

\(V_{int} = \frac{527}{8,95} = 58,86 m/h = 0,981 m/min\)

\(T-i = T_f = \frac{2}{3} \frac{330}{360} \frac{60}{0,981} = 0,62 h = 37 min\)

\(T_{irrig} = T_i + T_{int} + T_f = 0,62 + 8,95 + 0,62 = 10,2 h = 10h12min\)