| Camada (cm) |
Umidade volumétrica (cm³/cm³)
|
|
|---|---|---|
| Dia 05 | Dia 08 | |
| 0-10 | 0,28 | 0,25 |
| 10-20 | 0,31 | 0,27 |
| 20-30 | 0,35 | 0,33 |
| 30-40 | 0,39 | 0,36 |
2 A água no solo
Existem muitas maneiras que podemos definir o que é o solo. Para a engenharia da irrigação, talvez a melhor definição seja aquela que trata o solo como um sistema trifásico.
Sendo assim, podemos dizer que o solo é composto por partículas sólidas, líquidas e gasosas. A fase sólida, conhecida como matriz do solo, é constituída por partículas minerais e matéria orgânica. A fase líquida, ou solução do solo, compreende a água com solutos dissolvidos. Por fim, a fase gasosa, contém ar e outros gases.
Se fosse possível separar essas três fases, poder-se-ia visualizar algo como apresentado na Figura 2.1
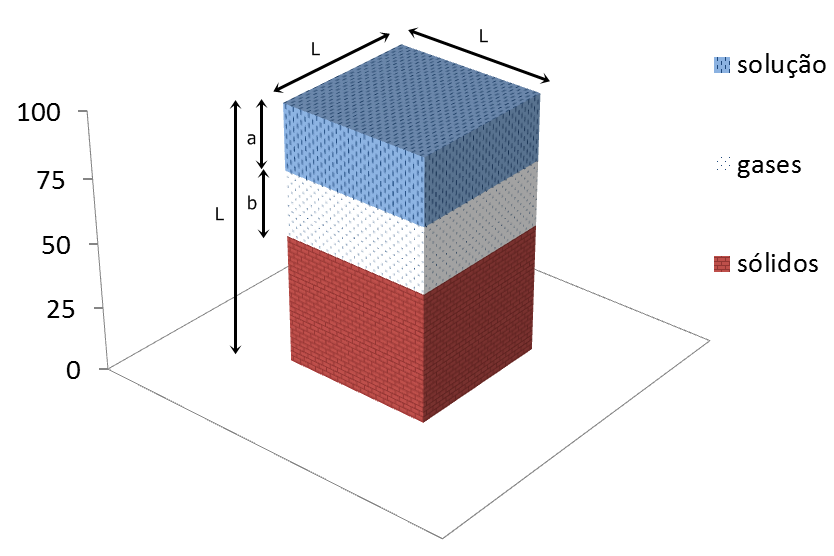
Em um volume típico de solo, a fase sólida ocupa a maior parte do espaço. As fases líquida e gasosa dividem o espaço poroso restante. Na escala temporal de uma safra agrícola, o volume de sólidos pode ser considerado praticamente constante. Já a proporção entre as fases líquida e gasosa elas é extremamente dinâmica, podendo variar em questão de minutos, dependendo das condições ambientais e do manejo do solo.
2.1 Relações massa-volume em um solo seco
Inicialmente, vamos considerar as relações massa-volume de um solo seco. A massa de um solo seco (Ms) é composta apenas pela massa da fase sólida, obtida após após a remoção da água do solo, geralmente por secagem em estufa. O volume total (Vt) do solo é a soma dos volumes ocupados por cada uma das fases (sólida, líquida e gasosa). Já o volume das partículas (Vp) do solo, é o volume ocupado apenas pela fase sólida.
2.1.1 Densidade do solo - Ds
A densidade do solo (Ds), também chamada de massa específica do solo, densidade aparente ou densidade global, é a relação entre a massa de solo seco (Ms) e o volume total (Vt) de uma amostra de solo.
\[ D_s = \frac{M_s}{V_t} \tag{2.1}\]
2.1.2 Densidade das partículas do solo - Dp
A relação entre a massa de solo seco (Ms) e o volume das partículas sólidas (Vp) é denominada densidade das partículas do solo (Dp). O valor médio da densidade das partículas de solos minerais é de aproximadamente 2,65 g/cm3. Este valor pode ser usado na maioria dos casos práticos.
\[ D_p = \frac{M_s}{V_p} \tag{2.2}\]
2.1.3 Porosidade - P
Outro importante parâmetro do solo é a porosidade (P), definida como a razão entre o volume de poros (o espaço não ocupado pelas partículas sólidas) e o volume total de solo. No entanto, é mais comum estimarmos a porosidade pela razão entre a densidade do solo (Ds) e a densidade das partículas (Dp).
\[ P = 1 - \frac{D_s}{D_p} \tag{2.3}\]
Observação:
É importante lembrar que as relações massa-volume do solo são influenciadas por diversos fatores, como a textura, a estrutura e o manejo do solo. Portanto, os valores de Ds e P podem variar consideravelmente entre diferentes tipos de solo e condições de manejo, como a compactação.
Exemplo 2.1 (Relações massa-volume em um solo seco) Considere uma amostra de solo indeformada retirada com um anel metálico com as seguintes dimensões: altura = 2,7 cm e diâmetro = 4,8 cm. Após secagam em estufa por 24h e 105ºC, a amostra foi pesada, e o valor obtido foi de 63,4 g. Calcule a densidade do solo e a porosidade desta amostra de solo.
Solução:
O volume de um cilindro é calculado por:
\(vol = \pi \cdot d^2/4 \cdot h\)
O volume do anel cilíndrico, que é igual ao volume do solo, é:
\(V_t = \pi \cdot 4,8^2/4 \cdot 2,7 = 48,86\ cm^3\)
A densidade do solo é calculada pela Equação 2.1:
\(D_s = \frac{63,4}{48,86} = 1,30\ g/cm^3\)
A porosidade é calculada pela Equação 2.3, com o valor padrão para Dp=2,65 g/cm3
\(P=1-\frac{1,30}{2,65} = 0,51 = 51 \%\)
2.2 Conteúdo de água no solo
O conteúdo de água no solo, também conhecido simplesmente como umidade do solo, é a quantidade de água presente no solo em um determinado momento. Existem diferentes maneiras de expressar o conteúdo de água no solo, sendo as mais comuns a umidade gravimétrica e a umidade volumétrica.
2.2.1 Umidade gravimétrica - U
A umidade gravimétrica, ou umidade em base de massa, representa a relação entre a massa de água (Ma) contida em uma amostra de solo e a massa desse mesmo solo seco (Ms):
\[ U = \frac{M_a}{M_s} \tag{2.4}\]
O resultado dessa equação representa a umidade em grama1 de água por grama de solo seco (g/g).
O métode de obtenção da umidade gravimétrica é conhecido como método direto. Amostras de solo úmido são retirados no campo e pesadas para determinação da massa do solo úmido (Mu). Após, são colocadas em estufa a 105ºC por, no mínimo, 24 horas, para secagem da amostra. Após esse período, é determinada a massa do solo seco (Ms). A massa da água (Ma) é calculada pela diferença Mu - Ms.
Exemplo 2.2 (Umidade gravimétrica) Considere a amostra de solo do Exemplo 2.1. Para uma amostra de solo úmido com massa igual a 76,3 g, calcular a umidade gravimétrica desta amostra de solo.
Solução:
- Massa de água
\(M_a=76,3-63,4 = 12,9\ g\)
- Umidade gravimétrica
\(U=\frac{12,9}{63,4} = 0,20\ g/g\)
O método direto é bastante preciso e relativamente simples. No entanto, apresenta o inconveniente de só permitir conhecer o valor da umidade após 24h. Para obter resultados mais rápidos, podem ser utilizados métodos indiretos com sensores, que fornecem leituras instantâneas da umidade do solo.
2.2.2 Umidade volumétrica - \(\theta\)
A umidade volumétrica (\(\theta\)), ou umidade em base de volume, é a relação entre o volume de água de uma amostra de solo e seu volume total. No entanto, podemos nos aproveitar de uma relação matemática e calcular a umidade volumétrica conhecendo a umidade gravimétrica (U) e a densidade do solo (Ds):
\[ \theta = U \cdot D_s \tag{2.5}\]
O resultado dessa equação representa a umidade em centímetro cúbico2 de água por centímetro cúbico de solo (cm3/cm3).
A umidade volumétrica (\(\theta\)) é mais conveniente para o manejo da irrigação, porque ela expressa a quantidade de água presente em um determinado volume de solo, o que facilita o cálculo da lâmina de água a ser aplicada na irrigação.
2.2.3 Grau de saturação - S
É a quantidade de água contida no solo em relação à saturação:
\[ S = \frac{\theta}{\theta_s} \tag{2.6}\]
Exemplo 2.3 (Umidade volumétrica) Determinar a umidade volumétrica do solo e o grau de saturação usando os valores do Exemplo 2.1 e Exemplo 2.2.
Solução:
Dos exemplos anteriores, temos Ds = 1,30 g/cm3, P = 0,51 e U = 0,20 g/g.
Logo, pela Equação 2.5:
\(\theta = 0,20 \cdot 1,30 = 0,26\)
E pela Equação 2.6:
\(S=\frac{0,26}{0,51} = 0,52\)
2.3 Armazenamento da água no solo
O armazenamento de água no solo é a quantidade de água retida em um determinado volume de solo. É um conceito fundamental para o manejo da irrigação, pois permite determinar a quantidade de água disponível para as plantas e a quantidade de água que precisa ser aplicada para repor a água perdida pela evapotranspiração.
A quantidade de água armazenada no solo pode ser expressa em termos de lâmina de água, que é a altura da camada de água que seria formada se toda a água presente em um determinado volume de solo fosse distribuída uniformemente sobre uma superfície plana.
Para se calcular o armazenamento de água no solo até uma profundidade z, basta multiplicar a umidade volumétrica média (\(\bar{\theta}\)) pela profundidade:
\[ A = \bar{\theta} \cdot z \tag{2.7}\]
Como \(\theta\) é adimensional, a unidade de A será definida pela unidade de z, geralmente em milímetros (mm) ou centímetros (cm).
Em perfis de solo com umidade heterogênea, onde a umidade varia ao longo da profundidade, o cálculo do armazenamento de água é realizado por meio da estratificação do perfil. O perfil é dividido em camadas de espessura \(\Delta\)z, e o armazenamento de água é calculado individualmente para cada camada, considerando a umidade volumétrica média (\(\bar{\theta}\)) da respectiva camada. Finalmente, somam-se os armazenamentos de água de todas as camadas para obter o armazenamento total no perfil.
\[ A = \sum (\bar{\theta} \cdot \Delta z) \tag{2.8}\]
É importante notar que o método de estratificação assume que a umidade é constante dentro de cada camada, o que pode não ser totalmente preciso em solos com alta variabilidade espacial. No entanto, esse método ainda fornece uma boa estimativa do armazenamento de água no solo e é amplamente utilizado na prática.
Exemplo 2.4 (Armazenamento da água no solo) A tabela abaixo mostra um exemplo de perfil de umidade do solo em dois dias diferentes:
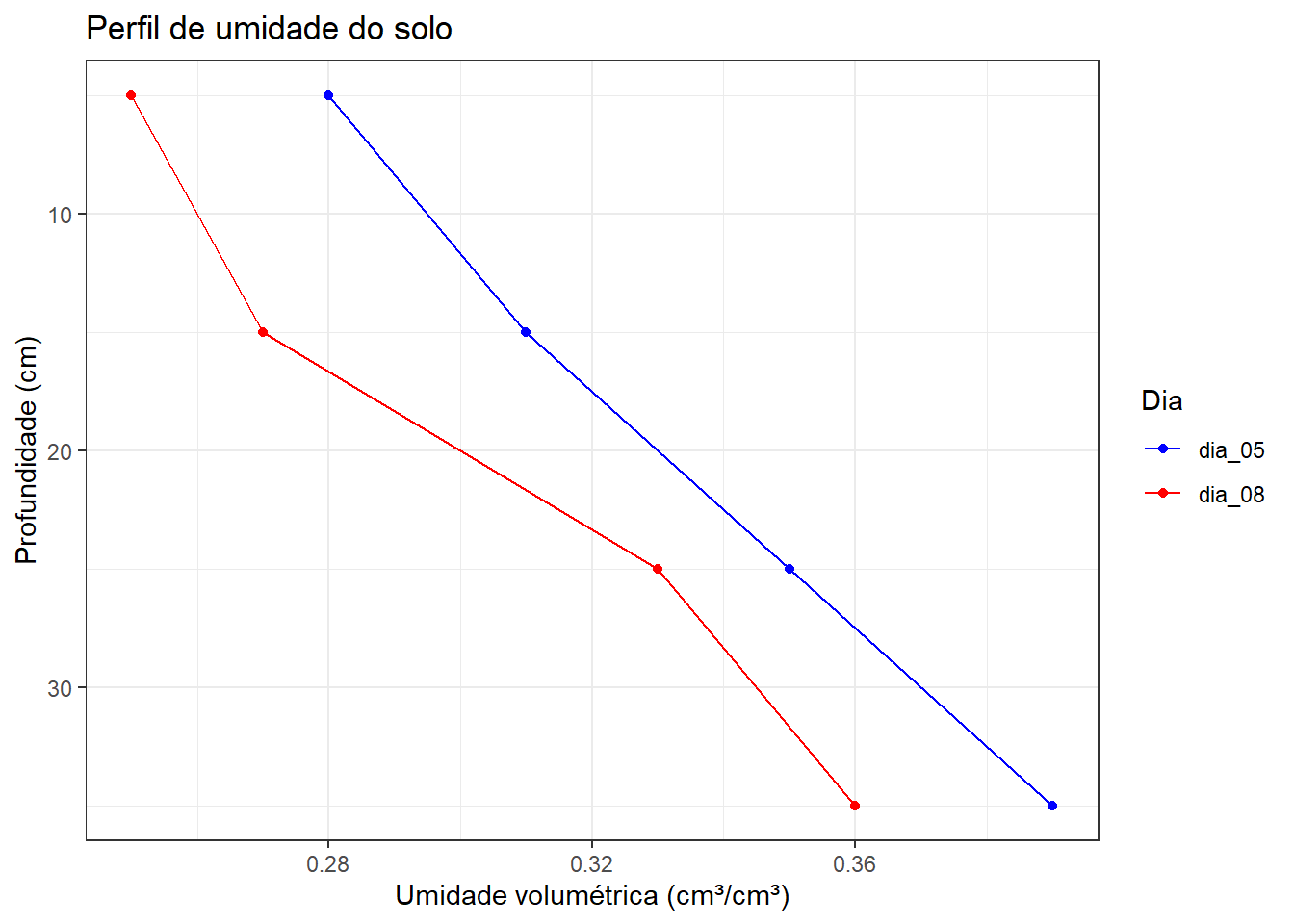
- Determine o armazenamento de água para os dias 05 e 08 para o perfil inteiro do solo.
Solução:
Dia 05: na camada 0-10 cm, o armazenamento é:
\(A_{0-10} = 0,28 \cdot (10-0)\ cm \cdot 10 = 28,00\ mm\)
- a multiplicação por 10 serve para transformar as unidades cm para mm.
A0-10 = 0,28 . (10-0) cm . 103 = 28,00 mm
Para as demais camadas:
10-20 cm: 31,00 mm
20-30 cm: 35,00 mm
30-40 cm: 39,00 mm
O armazenamento no dia 05 até 40 cm é:
A05 = 28,00 + 31,00 + 35,00 + 39,00 = 133,0 mm
Dia 08:
0-10 cm: 25,00 mm
10-20 cm: 27,00 mm
20-30 cm: 33,00 mm
30-40 cm: 36,00 mm
O armazenamento no dia 08 até 40 cm é:
A08 = 25,00 + 27,00 + 33,00 + 36,00 = 121,0 mm
b) Qual a diferença de armazenamento entre os dois dias?
A diferença no armazenamento é 133,0 - 121,0 = 12,0 mm.
c) Determine o armazenamento até 15 cm no dia 05.
O armazenamento até 15 cm deve ser calculado pela soma do armazenamento de 0-10 cm e de 10-15 cm
- Na camada 0-10 cm, o armazenamento é:
A0-10 = 0,28 . (10-0) cm . 10 = 28,0 mm
- Na camada 10-15 cm, o armazenamento é:
A10-15 = 0,31 . (15-10) cm . 10 = 15,5 mm
O armazenamento no dia 05 até 15 cm é:
A = 28,0 + 15,5 = 43,5 mm
2.4 Retenção da água no solo
A retenção de água no solo é a capacidade do solo de reter água em seus poros. A quantidade de água que um solo pode reter depende de vários fatores:
Textura do solo: Solos argilosos, com partículas menores, tendem a reter mais água do que solos arenosos.
Estrutura do solo: Solos com boa estrutura, com agregados bem formados, retêm mais água do que solos com estrutura pobre.
Matéria orgânica: A matéria orgânica aumenta a capacidade de retenção de água do solo.
Presença de sais: A presença de sais no solo pode reduzir a retenção de água.
A água proveniente da chuva ou irrigação penetra no solo, no processo de infiltração. Parte da água infiltrada pode percolar, ou seja, se deslocar verticalmente para baixo até grandes profundidades. Outra parte é retida nos poros do solo, resultado da interação de várias forças:
Forças de adesão: São as forças que atraem as moléculas de água para as partículas do solo.
Forças de coesão: São as forças que atraem as moléculas de água entre si.
Forças de capilaridade: São as forças que atuam nos microporos do solo, permitindo que a água suba contra a gravidade.
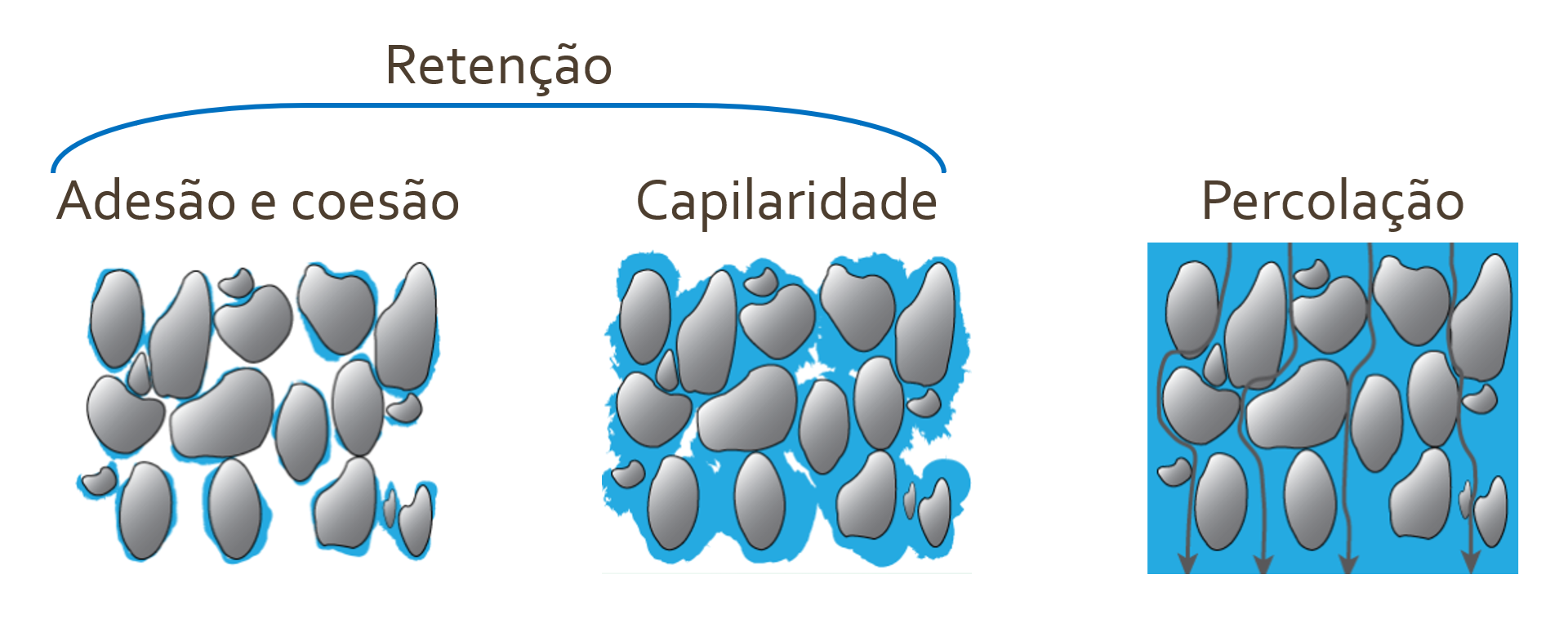
Essas forças determinam o nível de energia da água no solo, a capacidade de retenção e de movimentação, e, consequentemente, sua disponibilidade. A energia da água no solo, conhecida como potencial da água no solo, é influenciada pela interação entre as forças de adesão, coesão e capilaridade. As forças de adesão, que atraem as moléculas de água para as partículas do solo, e as forças de coesão, que atraem as moléculas de água entre si, atuam em conjunto para reter a água próxima às partículas do solo. As forças de capilaridade, por sua vez, permitem que a água se mova pelos microporos do solo, mesmo contra a força da gravidade, devido à diferença de potencial entre as diferentes zonas do solo. A adesão e coesão mantém a água fortemente retida às partículas do solo e não disponível às plantas. Já a capilaridade retém a água nos microporos e disponível para as plantas.
O potencial da água no solo é composto por vários componentes:
Potencial gravitacional \(\psi_g\): Relacionado à força da gravidade, que puxa a água para baixo.
Potencial de pressão \(\psi_p\): Relacionado à pressão hidrostática da água no solo em situação de saturação.
Potencial osmótico \(\psi_s\): Relacionado à presença de solutos dissolvidos na água do solo.
Potencial matricial \(\psi_m\): Relacionado à atração da água pelas partículas sólidas do solo (matriz do solo).
A água no solo tende a se mover de regiões com maior potencial para regiões com menor potencial. Em outras palavras, a água flui de áreas onde a energia da água é maior para áreas onde a energia da água é menor.
A retenção de água no solo é maior em solos com alto potencial matricial, ou seja, solos que exercem forte atração sobre as moléculas de água. Solos com textura fina, como os argilosos, tendem a ter maior potencial matricial e, portanto, maior capacidade de retenção de água.
Pelo fato dos solos irrigados geralmente não se encontrarem em situação de saturação 4, e o potencial osmótico apresentar um efeito muito pequeno, o potencial matricial se torna o mais importante componente do potencial da água no solo.
2.4.1 Curva característica da água no solo - Curva de retenção
A curva característica da água no solo, ou simplesmente curva de retenção, é uma relação entre o potencial matricial \(\psi_m\) e a umidade volumétrica \(\theta\) do solo, ou seja, descreve a relação entre a quantidade de água presente no solo e a energia com que essa água é retida. Essa curva é específica para cada tipo de solo.
A forma da curva característica varia de acordo com as propriedades do solo, como textura, estrutura e conteúdo de matéria orgânica. Solos arenosos, com poros maiores, tendem a ter curvas mais inclinadas, indicando que a água é retida com menos energia e é mais facilmente drenada. Solos argilosos, com poros menores, tendem a ter curvas mais planas, indicando que a água é retida com mais energia e é mais difícil de ser drenada.
Em solos com estrutura deteriorada, como solos compactados, há um deslocamento da curva para a esquerda e para baixo. Isso significa que, para um determinado potencial matricial, o solo compactado retém menos água do que o solo não compactado. A compactação também pode afetar a forma da curva, tornando-a mais inclinada na região de potenciais matriciais baixos.
A curva de retenção é obtida a partir de pares de valores de umidade volumétrica \(\theta\) e potencial matricial \(\psi_m\) obtidos em ensaios de laboratório. Há vários modelos matemáticos propostos para ajustar os dados de umidade e potencial, sendo o de Van Genuchten (1980) um dos mais amplamente utilizados:
\[ \theta = \theta_r + \frac{\theta_s-\theta_r}{(1+(\alpha \cdot |\psi_m|)^n)^{(1-1/n)}} \tag{2.9}\]
em que:
- \(\theta_s\): umidade na saturação.
- \(\theta_r\): umidade residual.
- \(\alpha\), n: parâmetros estimados no ajuste.
A figura abaixo mostra as curvas de retenção para dois tipos de solo: argiloso e arenoso.
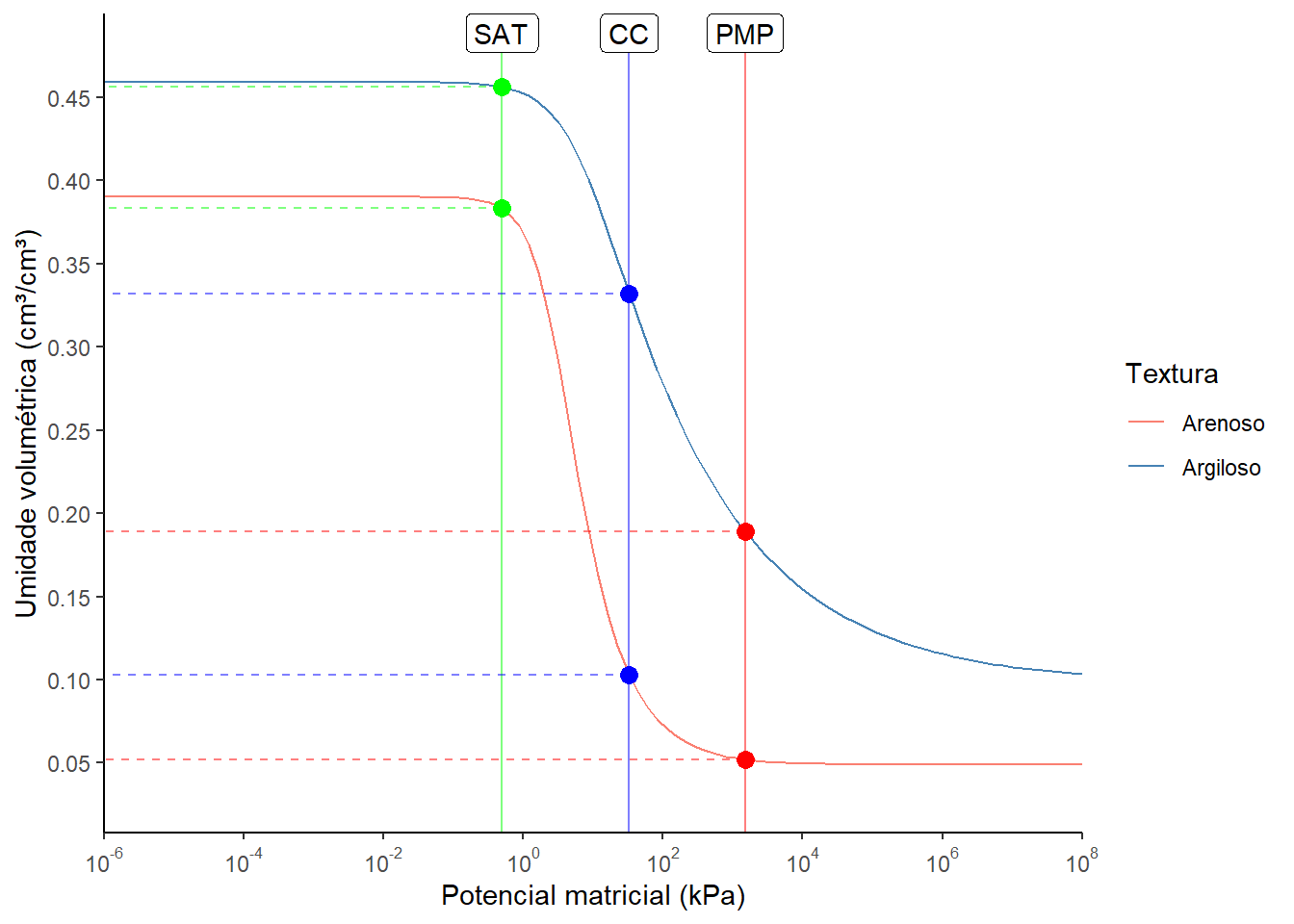
No solo arenoso, a curva de retenção é mais inclinada, o que significa que ele libera água mais facilmente em resposta a mudanças no potencial matricial. Isso ocorre porque solos arenosos têm poros maiores, e a água é retida com menos força. Já no solo argiloso, a curva de retenção é mais plana, indicando que ele retém água com mais força e a libera mais lentamente. Os solos argilosos têm maior capacidade de retenção de água do que solos arenosos. Já os solos arenosos são mais propensos à drenagem e à perda de água do que solos argilosos.
Exemplo 2.5 (Curva de retenção) Considere as curvas de retenção da Figura 2.3, que são representada pelos seguintes parâmetros da equação de Van Genuchten (Equação 2.9 - potencial em unidade de kPa):
| Tipo de solo | θs | θr | ɑ | n |
|---|---|---|---|---|
| Argiloso | 0,4590 | 0,0980 | 0,1526 | 1,2531 |
| Arenoso | 0,3900 | 0,0490 | 0,3544 | 1,7458 |
- Qual a umidade do solo quando o potencial é de 33 kPa e de 1500 kPa para os dois tipos de solo?
- Solo argiloso:
\(\theta_{33kPa}\) = 0,3318 cm3/cm3
\(\theta_{1500kPa}\) = 0,1892 cm3/cm3
- Solo arenoso:
\(\theta_{33kPa}\) = 0,1032 cm3/cm3
\(\theta_{1500kPa}\) = 0,05216 cm3/cm3
- Qual a lâmina de água que deve ser aplicada até 35 cm de profundidade quando o solo estiver com um potencial de 100 kPa para que a umidade seja elevada até o potencial de 33 kPa? Responda para os dois tipos de solo.
- Solo argiloso
\(\theta_{100kPa}\) = 0,2779 cm3/cm3
\(\theta_{33kPa}\) = 0,3318 cm3/cm3
Lâmina = (0,3318 - 0,2779) . 35 cm . 10 = 18,9 mm
- Solo arenoso
\(\theta_{100kPa}\) = 0,0728 cm3/cm3
\(\theta_{33kPa}\) = 0,1032 cm3/cm3
Lâmina = (0,1032 - 0,0728) . 35 cm . 10 = 10,6 mm
2.5 Disponibilidade de água no solo
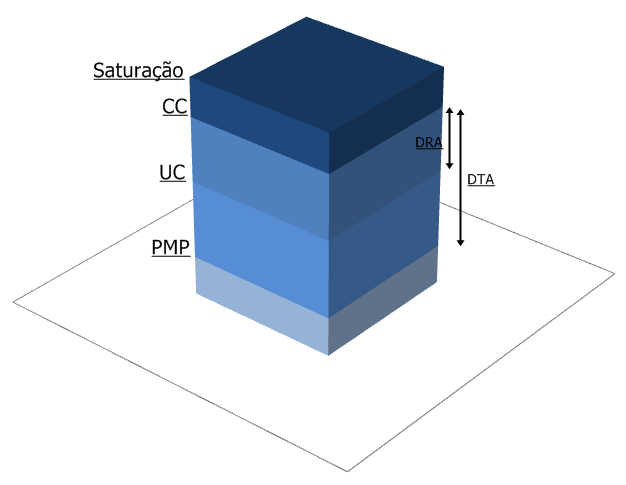
O solo é capaz de reter e armazenar água, mas nem toda água contida em um solo fica disponível para utilização pelas plantas. É muito comum definirmos dois limites para a disponibilidade da água no solo.
O limite inferior é conhecido como Ponto de Murcha Permanente (PMP) e corresponde à tensão de 1500 kPa. Nesse ponto, a água está fortemente retida no solo pelas forças de adesão e coesão e não
As plantas não são capazes de retirar água do solo quando a umidade está abaixo do PMP5.
O limite superior é chamado de Capacidade de Campo (CC). A tensão correspondente a CC é muito variável, em função da cultura, tipo de solo e demanda da atmosfera. Valores comuns estão entre 10 e 30 kPa. Considera-se que as culturas não conseguem aproveitar a água do solo retida acima da CC pois esta drena muito rapidamente 6.
A disponibilidade total de água no solo (DTA) corresponde à água armazenada no intervalo entre os limites inferior e superior. É expressa em altura de lâmina de água por profundidade de solo, por exemplo, milímetro de água por milímetro de solo, ou então, milímetro de água por centímetro de solo (multiplicar por 10 na Equação 2.10).
\[ DTA = (\theta_{CC} - \theta_{PMP}) \tag{2.10}\]
Solos com textura grossa, como areias, têm menor DTA, enquanto solos com textura fina, como argilas, têm maior DTA (Tabela 2.1). Isso ocorre porque solos argilosos têm maior capacidade de retenção de água do que solos arenosos.
| Textura | DTA |
|---|---|
| Grossa | 0,4 a 0,8 |
| Média | 0,8 a 1,6 |
| Fina | 1,2 a 2,4 |
| Fonte: Carvalho et al, 2014 | |
A água disponível (AD) no solo, também conhecida como capacidade total de água (CTA) ou capacidade de água disponível (CAD), corresponde à disponibilidade de água até uma determinada profundidade. Geralmente, considera-se a profundidade efetiva do sistema radicular (Z) para o cálculo da AD, que representa a profundidade que contém pelo menos 80% das raízes das plantas. Em outras palavras, a AD indica a água armazenada que as plantas podem acessar em um determinado solo.
\[ AD = DTA \cdot Z \tag{2.11}\]
A água facilmente disponível (AFD), também é conhecida como capacidade real de água no solo (CRA) é definida como a fração da água disponível que as plantas podem utilizar sem afetar significativamente a sua produtividade.
\[ AFD = AD \cdot f \tag{2.12}\]
O fator de disponibilidade f varia entre 0,2 e 0,8. Os valores menores são usados em culturas mais sensíveis ao déficit hídrico e os maiores nas culturas mais resistentes (Tabela 2.2).
| Grupo de plantas | f |
|---|---|
| Verduras e Legumes | 0,2 a 0,6 |
| Frutas e Forrageiras | 0,3 a 0,7 |
| Grãos e Algodão | 0,4 a 0,8 |
| Fonte: Carvalho et al, 2014 | |
Combinando todas as equações anteriores (Eq. 2.10, Eq. 2.11 e Eq. 2.12), definimos a AFD como na Equação 2.13:
\[ AFD = (\theta_{CC} - \theta_{PMP}) \cdot Z \cdot f \tag{2.13}\]
Exemplo 2.6 (Disponibilidade da água no solo.) Considere um solo com as seguintes características:
- Umidade na capacidade de campo: \(\theta_{cc}\) = 0,283 cm3/cm3
- Umidade no ponto de murcha permanente: \(\theta_{pmp}\) = 0,069 cm3/cm3
Calcular a DTA, AD e AFD considerando um cultivo de milho, cuja profundidade efetiva do sistema radicular é Z = 50 cm e o fator de disponibilidade é f = 0,5.
Solução
A DTA é calculada pela Equação 2.10:
\(DTA = (0,283 - 0,069) \cdot 10 = 2,14\ mm/cm\)7
A AD é calculada pela Equação 2.11:
\(AD = 2,14 \cdot 50 = 107,00\ mm\)
A AFD é calculada pela Equação 2.12:
\(AFD = 107,0 \cdot 0,5 = 53,50\ mm\)
A AFD também pode ser calculada pela Equação 2.13, que resulta no mesmo valor:
\(AFD = (0,283 - 0,069) \cdot 10 \cdot 50 \cdot 0,5 = 53,50\ mm\)
ou outra unidade de massa↩︎
ou outra unidade de volume↩︎
para transformar unidades↩︎
exceção é o arroz irrigado por inundação↩︎
Apesar dessa afirmação não ser totalmente verdadeira, pois existem exceções, continua sendo uma boa metodologia, ao menos para a agricultura irrigada.↩︎
Assim como para o PMP, esta é uma definição muito simplificada, mas que atende muitas situações na agricultura irrigada.↩︎
leia-se mm de água por centímetro de solo.↩︎