
6 Avaliação de Sistemas de Irrigação Pressurizada
A valiação de sistemas de irrigação pode ter como objetivo:
- avaliar os efeitos da uniformidade na quantificação da lâmina de irrigação;
- verificar a necessidade de troca de componentes;
- avaliar a gestão dos recursos hídricos;
- avaliar o retorno financeiro sobre o investimento;
As medidas de avaliação estão relacionada à eficiência e uniformidade
6.1 Eficiência
A eficiência da irrigação pode ser definida como a razão entre a água consumida pelo processo de evapotranspiração e a água retirada para a irrigação.
A água não aproveitada pode ser considerada como perda. No entanto, este conceito deve ser aplicado em uma escala adequada, mais comumente, de parcela irrigada.
De modo geral, a eficiência da irrigação pode ser particionada em eficiência de aplicação e eficiência de distribuição.
6.1.1 Eficiência de aplicação
É a fração da água aplicada que permaneceu disponível para infiltrar no solo.
\(E_a = \frac{L_i}{L_a}\)
em que:
- \(L_i\) - lâmina de água infiltrada
- \(L_a\) - lâmina de água aplicada
A perda por evaporação e deriva é igual a 1-Ea.
6.1.2 Eficiência de distribuição
É a fração de água infiltrada que permaneceu disponível na zona radicular da cultura.
\(E_d = \frac{L_s}{L_i}\)
em que:
- \(L_s\) - lâmina de água útil armazenada
- \(L_i\) - lâmina de água infiltrada
A perda por percolação é igual a 1-Ed.
6.1.3 Eficiência de irrigação
É a fração da água aplicada que é armazenada no perfil do solo e disponível para a cultura.
\(E_a = \frac{L_s}{L_a}\)
em que:
- \(L_s\) - lâmina de água útil armazenada
- \(L_a\) - lâmina de água aplicada
6.2 Uniformidade
A medida de uniformidade expressa a variabilidade da lâmina de irrigação aplicada no solo. Um sistema de irrigação que não aplica água com uniformidade irá aplicar água em excesso em algumas áreas enquanto que em outras áreas irá aplicar água em déficit.
Muitas fórmulas matemáticas são utilizadas para descrever a uniformidade de um sistema de irrigação. O coeficiente de uniformidade de Christiansen (CUC) é o mais utilizado, especialmente para sistemas de irrigação por aspersão,
A fórmula utiliza o desvio média absoluto como medida de dispersão:
\[ CUC_\% = \left(1 - \frac{\sum|X_i - \overline X|}{\sum X_i}\right)\cdot 100 \]
em que:
- \(X_i\) - lâmina aplicada no ponto i
- \(\overline X\) - lâmina média aplicada
Em geral, valores acima de 85% são aceitáveis para sistemas de aspersão. Valores abaixo deste podem ser admitidos caso a precipitação seja relevantes durante o ciclo da cultura.
Os valores da lâmina aplicada são obtidos em ensaios como o demonstrado na Figura Figura 6.1).

Para pivô central, a lâmina em cada ponto deve ser ponderada pois a área que cada coletor representa é maior a partir do ponto central do pivô. A equaçao fica assim:
\[ CUC_\% = \left(1 - \frac{\sum ( S_i \cdot |X_i - \overline X|)}{\sum(X_i \cdot S_i)} \right) \cdot 100 \] A lâmina média é calculada pela seguine equação:
\[ \overline X = \frac{\sum X_i \cdot S_i}{\sum S_i} \]
em que:
- \(X_i\) - lâmina aplicada no ponto i
- \(\overline X\) - lâmina média aplicada
- \(S_i\) - distância do coletor ao ponto do pivô

No caso dos coletores estarem dipostos em espaçamentos equidistantes, a distância do coletor ao ponto do pivô pode ser substituída pelo número de ordem do coletor.
Exemplo 6.1 (Coeficiente de uniformidade.) Calcular o CUC com os dados abaixo:
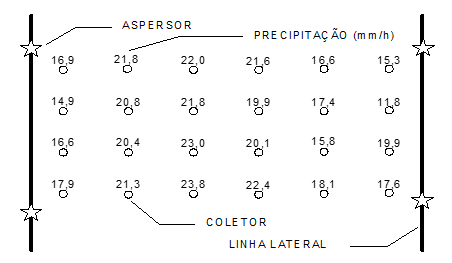
\(\overline X = \frac{16,9 + 21,8 + ... + 17,6}{24} = 19,07\)
\(CUC_\% = \left(1 - \frac{|21,8-19,07| + |16,9-19,07| + ... + |17,6-19,07|}{16,9+21,8+...+17,6}\right)\cdot 100 = 86,51\%\)