7 Projeto de Sistemas de Irrigação Pressurizada
7.1 Microirrigação
O principal objetivo do dimensionamento é proporcionar uma aplicação de água uniforme e eficiente às plantas e atender a demanda de água destas. Além disso, deve demonstrar viabilidade financeira com o menor custo de instalação e operação que satisfaçam as condições acima.
Via de regra, o projeto deve ser o mais simples possível. Também deve satisfazer o nível de especialização do irrigante. A confiabilidade do sistema também é muito importante.
7.2 Dimensionamento agronômico de sistemas de microirrigação
O dimensionamento agronômico tem como objetivo determinar a máxima lâmina de irrigação que deverá ser aplicada pelo sistema no momento do ciclo da cultura em que a evapotranspiração é máxima. Este valor de evapotranspiração diária é encontrado em estudos relacionados ao consumo hídrico das culturas.
O turno de rega pode ser calculado a partir de dados do solo e da planta, ou então, definido a priori de modo a garantir o alto potencial de evapotranspiração da cultura. Em todo caso, o turno de rega é pequeno (alta frequência) variando de 1 a 3 dias. Os menores valores são utilizados para culturas mais sensíveis à falta de água (olerícolas em geral) e os maiores valors para culturas mais tolerantes (frutíferas em geral).
A lâmina máxima de irrigação é calculada pela multiplicação da evapotranspiração máxima diária pelo turno de rega:
\(Lam_{loc} = ETc_{max} \cdot TR\)
Além disso, a evapotranspiração deve ser corrigida para a irrigação localizada, pois esta não molha a área total. A ETc é corrigida por um fator KL que, por sua vez, depende da área molhada ou da área sombreada pela cultura.
\(ETc_{loc} = ETc \cdot K_{L}\)
O fator KL depende da porcentagem de área molhada ou de área sombreada (qual tiver o maior valor). A porcentagem de área molhada/sombreada (P) é calculada por:
\(P = \frac{A_{m/s}}{A_T}\)
em que:
- Am/s - área molhada/sombreada
- AT - área total
O fator KL dever ser calculado por um dos seguintes métodos:
- Método de Keller (1978) – culturas mais densas
\(K_L = P + 0,15 \cdot (1-P)\)
- Método de Fereres (1981) – culturas com maior espaçamento
- Se \(P\geq0,65\): \(K_L = 1,0\)
- Se \(0,20 < P < 0,65\): \(K_L = 1,09 \cdot P + 0,30\)
- Se \(P\leq0,20\): \(K_L = 1,94 \cdot P + 0,10\)
- Método de Keller e Bliesner (1990) – uso geral/café mecanizado
\(K_L = 0,1 \cdot \sqrt{P \cdot 100}\)
Vejamos alguns exemplos para facilitar a compreensão destes conceitos:
Exemplo 7.1 Considere um plantio de morango em canteiros com 90 cm de largura e carreadores (entre canteiros) de 40 cm. O espaçamento do morango é de 30 cm entre fileiras de plantio. A irrigação por gotejamento é distribuída em 2 linhas entre as fileiras de morango, sendo que forma uma faixa molhada contínua. A evapotranspiraçao máxima da cultura foi determinada em 5,2 mm/dia. O turno de rega foi definido em 2 dias. Qual a porcentagem de área molhada e a lâmina de irrigação máxima diária?
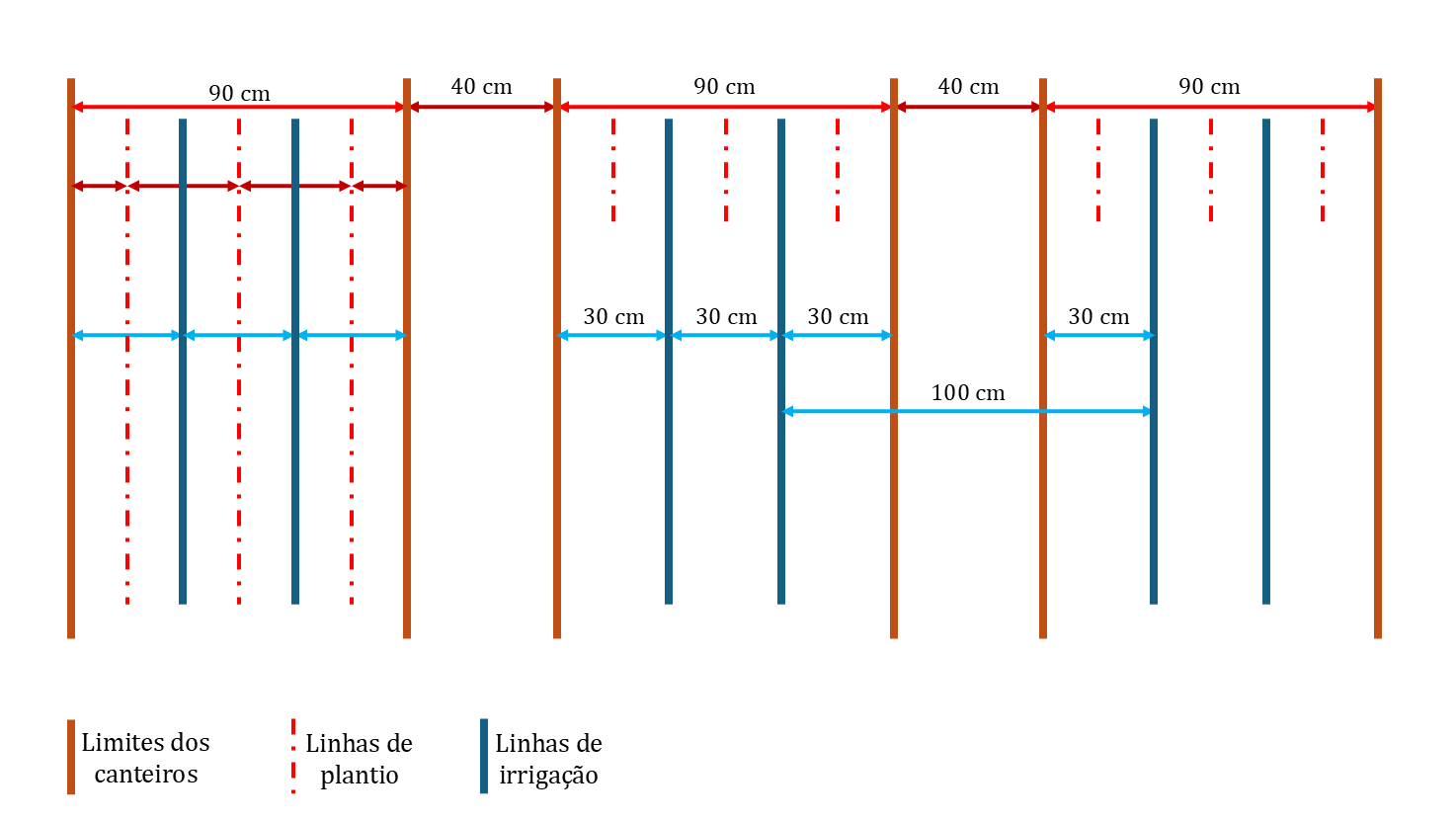
Porcentagem de área molhada:
\(P = \frac{90}{90+40} = 0,692\)
Fator de correção para irrigação localizada:
\(K_L = 0,692 + 0,15 \cdot (1-0,692) = 0,738\)
Evapotranspiração da irrigação localizada:
\(ETc_{loc} = ETc \cdot K_L = 5,2 \cdot 0,738 = 3,84 mm/dia\)
Lâmina de irrigação máxima diária:
\(Lam_{loc} = 3,84 mm/dia \cdot 2 dias = 7,68 mm\)
Exemplo 7.2 Considere um plantio de citrus no espaçamento de 4,0 x 7,0 m. O diâmetro da projeção da copa das árvores é de 3,2 m. A evapotranspiração máxima é de 4,7 mm/dia. O turno de rega foi definido em 3 dias. Qual a porcentagem de área molhada e a lâmina de irrigação máxima diária?
Porcentagem de área molhada:
\(P = \frac{\pi \cdot 3,2^2/4}{4,0 \cdot 7,0} = 0,251\)
Fator de correção para irrigação localizada:
\(K_L = 1,09 \cdot 0,251 + 0,30 = 0,574\)
Evapotranspiração da irrigação localizada:
\(ETc_{loc} = ETc \cdot K_L = 4,7 \cdot 0,574 = 2,70 mm/dia\)
Lâmina de irrigação máxima diária:
\(Lam_{loc} = 2,70 mm/dia \cdot 3 dias = 8,1 mm\)
7.3 Dimensionamento hidráulico de sistemas de microirrigação
O principal objetivo do dimensionamento hidráulico é determinar quais emissores serão utilizados, qual o material das tubulações e seus respectivos diâmetros, a pressão necessária em vários pontos do sistema e as especificações do conjunto motobomba necessário para pressurizar o sistema.
O primeiro passo consiste em selecionar um emissor adequado para atender às características do projeto. É o momento mais importante do dimensionamento hidráulico e requer uma combinação de critérios objetivos e subjetivos.
De modo geral, a seleção será feita com base na vazão do emissor. Esta será utilizada para determinar a intensidade de aplicação do emissor, o tempo de irrigação e a quantidade de subunidades do sistema.
A intensidade de aplicação é calculada por:
\(I_a = \frac{Q_{emissor}}{espaçamento}\)
em que: Qemissor - vazão do emissor
O espaçamento a ser utlizado pode ser o espaçamento da cultura ou o espaçamento entre emissores, dependendo se houver a formação de uma faixa contínua irrigada ou não.
O tempo de irrigação em cada posição é calculado por:
\(T_{irrig} = \frac{Lam_{loc}}{Ia}\)
O número máximo de subunidades em que o sistema pode ser dividido é calculado por:
\(N_{su} = \frac{TR \cdot Jornada}{T_i}\)
em que a Jornada de trabalho é a quantidade de horas do dia disponíveis para a irrigação.
Em seguida, devemos criar o layout da divisão da área irrigada em subunidades.
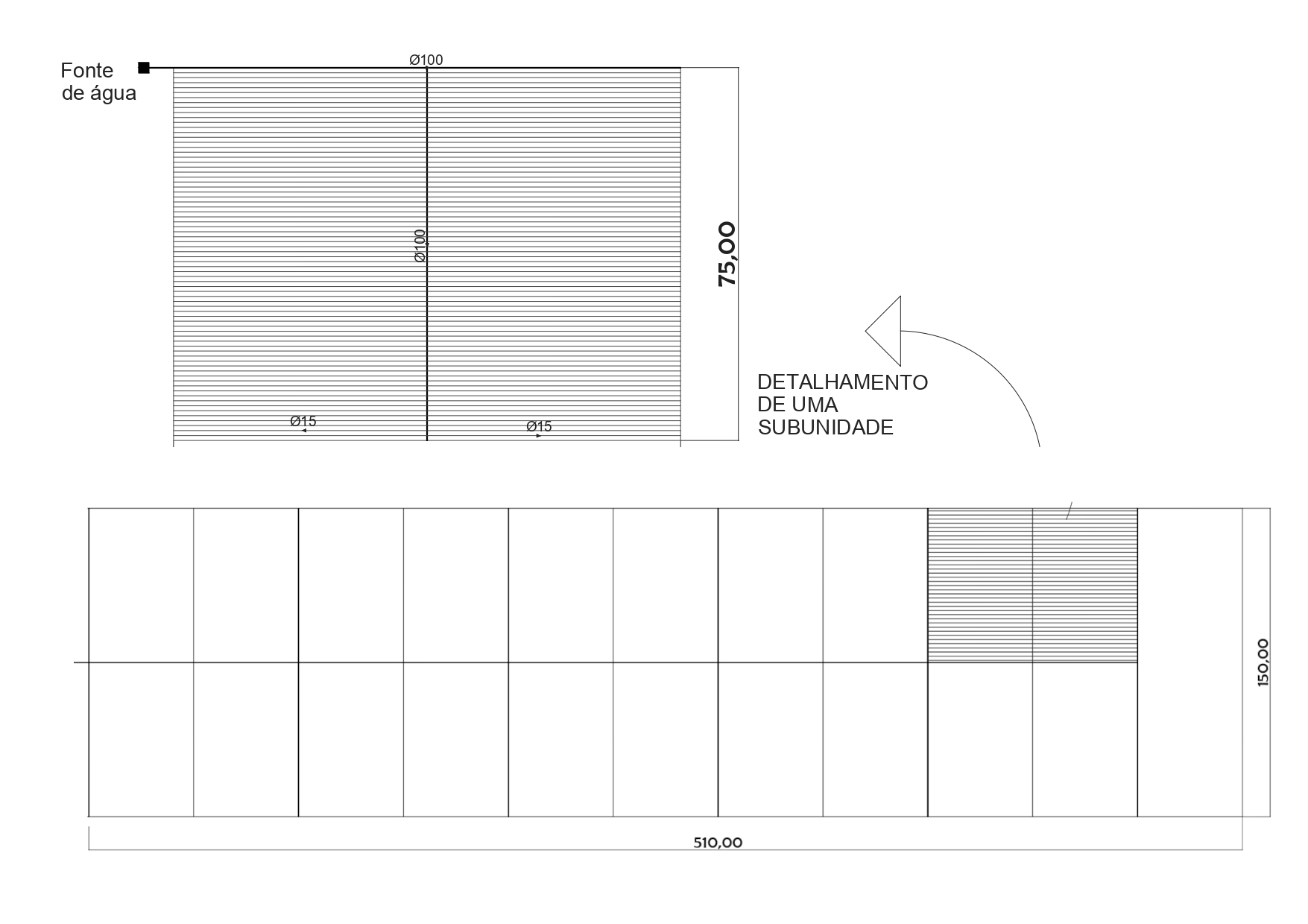
O valor obtido para a quantidade máxima de subunidades deve balizar a decisão nesse ponto, mas não deve ser considerado um valor rígido. Uma quantidade excessivamente grande de subunidades é custosa e cria dificuldades no manejo.
Nesse momento também é muito importante desenhar o layout das linhas de irrigação: adutora, principal, derivação e lateral. O comprimento destas linhas devem aparecer claramente no layout do sistema de irrigação (veja Figura Figura 7.1).
Exemplo 7.3 Considere as seguintes especificações de um projeto:
- Vazão do emissor = 1 L/h
- Espaçamento = 0,25 x 1,0 m
- Lâmina de irrigação máxima diária = 4,8 mm
- Turno de rega = 1 dia
- Jornada = 16 h
Calcule o número máximo de subunidades.
\(I_a = \frac{1 L/h}{0,25 \cdot 1,0 m^2} = 4 mm/h\)
\(T_{irrig} = \frac{4,8 mm}{4 mm/h} = 1,2 h\)
\(N_{su} = \frac{1 \cdot 16}{1,2} = 13 subunidades\)
Na Figura @ref(fig:7-croqui) vemos um layout dividido em 10 subunidades, compatível com as especificações deste projeto.
7.3.1 Dimensionamento da subunidade de microirrigação
A subunidade de microirrigação é composta, geralmente, por uma linha de derivação de onde partem as linhas laterais. Para a aplicação uniforme de água na subunidade, são fixadas variações máximas de vazão entre os emissores. O critério mais comumente utilizao é permitir uma variação máxima de 10% na vazão dos emissores.
Para alcançar essa variação de vazão, deve-se atingir uma variação máxima na pressão entre os emissores. Para emissores não regulados, a variação de pressão é calculada pela seguinte equação:
\[ H_{var} = Q_{var}^{(1/x)}-1 \]
em que
- Qvar - variação de vazão entre os emissores: qmax/qmin
- x - expoente da relação pressão-vazão do emissor
Para emissores autocompensantes, a variação de pressão é dada pelo intervalo de pressão de funcionamento do emissor, obtido junto ao catálogo deste.
Para uma variação máxima de 10% na vazão (Qvar= 1,1), qual a variação de pressão que pode ser permitida para emissores cujo expoente da relação pressão-vazão é igual a 0,50.
\[ H_{var} = 1,1^{(1/0,50)}-1 = 0,21 \]
A variação de pressão é de 21%
O diâmetro mínimo das linhas de derivação e lateral é calculado por meio das fórmulas de perda de carga (Fórmula Universal, Equação de Hazen-Willians, Equação de Flamant, etc.) a partir de informações do número de emissores em cada linha lateral, número de linhas laterais partindo da linha de derivação, comprimento das linhas de derivação e laterais e vazão média do emissor.
O diâmetro calculado deve ser utilizado como indicativo na seleção do diâmetro comercial. Deve-se sempre selecionar um diâmetro comercial superior ao calculado para garantir a máxima variação de vazão adotada no projeto.
7.3.2 Dimensionamento da linha principal e secundárias
No dimensionamento destas linhas, o critério econômico é amplamente utilizado. Deve-se chegar a um ponto de equilíbrio entre o custo de aquisição das tubulações e o custo de operação devido às perdas de carga. Para isso, um ponto de partida é o critério da velocidade máxima de 2 m/s da água nas tubulações.
\[ D=\sqrt{\frac{4 \cdot Q}{\pi \cdot 2,0}} \] ### Dimensionamento do conjunto motobomba
Consiste na seleção de um conjunto motobomba adequado que atenda às necessidades de vazão e de altura manométrica requeridas no projeto de microirrigação.
7.4 Análise financeira do dimensionamento de sistemas de microirrigação
Uma etapa fundamental do dimensionamento é a análise dos custos totais do projeto de irrigação. Estes custos são compostos pelo custo do investimento somado ao custo operacional.
O custo do investimento é geralmente gasto antes do início da operação do sistema em uma parcela única. Além disso, existem vários custos de manutenção relacionados à substituição de componentes do sistema, principalmente dos emissores.
O custo operacional é compostos principalmente pelo custo da energia elétrica despendida na operação do sistema, e só incide quando o sistema é de fato utilizado.
o custo total do projeto pode ser estimado pela transformação do fluxo de caixa em um valor presente (VPL) ou em uma série uniforme de pagamentos anuais.