2.3 Armazenamento da água no solo
A lâmina aplicada multiplicada pela área de interceptação da lâmina nos fornecerá o volume equivalente. Assim, define-se 1 mm de lâmina de água como sendo um volume de 1 L distribuído em uma área de 1 m2. Da mesma forma, 1 mm é igual a 10 m3/ha.
A lâmina de água armazenada (h) em um perfil solo homogêneo até uma profundidade Z é calculada por:
\[\begin{equation} h = \theta \cdot Z \tag{2.9} \end{equation}\]
No entanto, é mais comum encontrar perfis de solo heterogêneos. Nestes casos, o armazenamento é calculado estratificando o perfil de solo em pequenas camadas homogêneas (\(\Delta\) Z):
\[\begin{equation} h=\sum \bar{\theta} \cdot \Delta Z \tag{2.10} \end{equation}\]
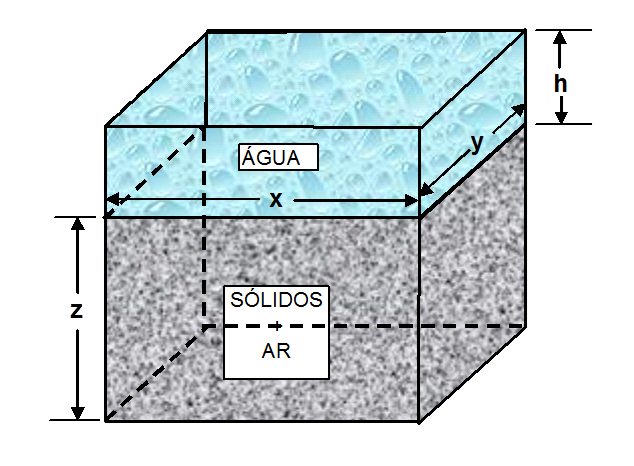
Figura 2.2: Armazenamento da água no solo.
Exemplo 2.2 Considere o perfil de umidade da tabela abaixo:
| Profundidades (cm) | Umidade em 28/01 (cm3/cm3) | Umidade em 31/01 (cm3/cm3) |
|---|---|---|
| 00 – 15 | 0,331 | 0,295 |
| 15 – 30 | 0,368 | 0,351 |
| 30 – 45 | 0,410 | 0,393 |
| 45 – 60 | 0,484 | 0,474 |
| 60 – 75 | 0,439 | 0,435 |
| 75 – 90 | 0,421 | 0,421 |
| 90 – 105 | 0,396 | 0,422 |
| 105 – 120 | 0,370 | 0,400 |
Determine o armazenamento de água para os dias 28/01 e 31/01 por camada e para o perfil inteiro do solo.
Determine o consumo de água entre esses dias.
\(h_{28/01} = 0,331 \cdot 150 + 0,368 \cdot 150 + ... + 0,370 \cdot 150 = 482,85 mm\)
\(h_{31/01} = 0,295 \cdot 150 + 0,351 \cdot 150 + ... + 0,400 \cdot 150 = 478,65 mm\)
\(consumo = 482,85 - 478,65 = 4,2 mm\)