2.4 Potencial da água no solo
A água no solo está sujeita a forças de diferentes origens e de intensidade variável, resultando no chamado potencial da água no solo. O potencial total da água no solo (\(\psi\)t) é composto dos seguintes componentes:
- Mátrico (\(\psi\)m): resulta dos efeitos combinados dos fenômenos da capilaridade e adsorção dentro da matriz do solo quando este se apresenta não saturado.
- Osmótico (\(\psi\)s): determinado pela presença de solutos na água.
- Pressão (\(\psi\)p): definido pela pressão hidrostática de uma coluna de água formada em um solo saturado.
- Gravitacional (\(\psi\)g): determinado pela posição relativa do ponto de medição.
A relação fundamental entre o conteúdo de água no solo e o potencial mátrico é chamada curva de retenção da água no solo. Tipicamente, a curva de retenção é descrita por equações contínuas não lineares, e como o potencial mátrico se estende por várias ordens de magnitude, ela é frequentemente plotada em escala logarítmica. São muitas as funções matemáticas que descrevem a curva de retenção, sendo mais comumente utilizada a equação de Van Genuchten:
\[\begin{equation} \frac{\theta - \theta_r}{\theta_s - \theta_r} = \left (\frac{1}{1+(\alpha \cdot |\psi_m|)^n} \right)^m \tag{2.11} \end{equation}\]
Em que:
- \(\theta\) – conteúdo de água volumétrico;
- \(\theta\)s – conteúdo de água na saturação;
- \(\theta\)r – conteúdo de água residual;
- |\(\psi\)m| - valor absoluto (sempre positivo) do potencial mátrico;
- \(\alpha\), m e n - parâmetros de ajuste dependentes do formato da curva de retenção; \(\alpha\)>0; n>1; 0<m<1.
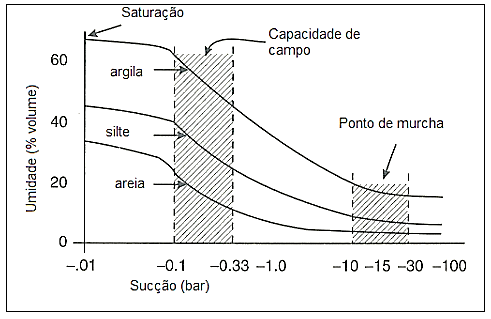
Figura 2.3: Curva de retenção da água no solo.
Exemplo 2.3 Considere a curva de retenção da figura abaixo. A capacidade de campo corresponde a um potencial mátrico de 0,1 atm. A cultura a ser irrigada é o feijoeiro (Z=50 cm) e as irrigações devem ser reiniciadas quando o potencial mátrico atingir 0,5 atm. Determinar a lâmina de água a ser aplicada para elevar a umidade até a capacidade de campo. Considerar ds=1,4.
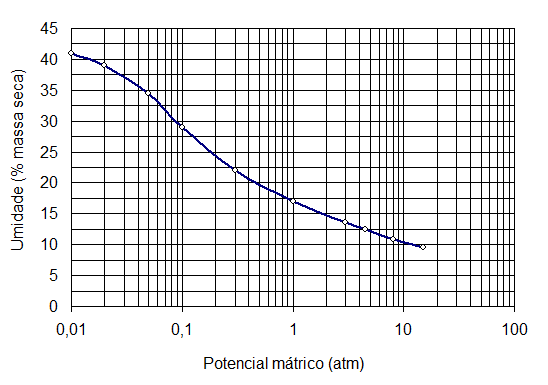
Analisando o gráfico:
\(\theta_{CC} = 29 \%\)
\(\theta_{CR} = 18 \%\)
\(Lamina = (0,29-0,18) \cdot 1,4 \cdot 500 = 77 mm\)